Segmentos
- Se tiene los dos puntos colineales P, M, Q y R; si M es punto medio de PQ, Q es punto medio de PR y PM = 5, calcular PR.
2. Calcular MN; si: AC+BD=20; M y N son puntos medios de AB y CD respectivamente.
3. En la figura, calcular X, si: AD = 36
4. En el gráfico AB es congruente con BC; según se muestra; determine el valor de X.
5. Calcular BC:
6. Sobre una recta se toman los puntos consecutivos A, B, C y D tal que AC=12u, BD= 16u y B es punto media de AC. Hallar CD.
7. Se tienen los puntos colineales y consecutivos P, Q, R y S de manera que: PR+QS= 17m y QR=6m. Hallar: PS.
7. Los puntos A, B, C y D se encuentran sobre una recta; de modo que AC=BD, AD=2BC. Halla: CD/BC
8. Sobre CB se ubican los puntos consecutivos “A” y “M” (en ese orden); siendo “M” punto medio de CB. Calcule AM : Si AB – AC = 30.
9. Se tienen los puntos colineales P,Q,R y S. Si: PQ=3QR=4RS y PS=19. Hallar QR.
10. Sobre una línea recta se consideran los puntos A,B,C y D tal que: AD=2AC, BC=4AB y CD=9dm. Hallar BD.
11. En el gráfico, B y D son puntos medios de AC y CE respectivamente. Calcula la medida de AE.
12. En el gráfico, Q es punto medio de PR. Calcula la medida de RS.
13. Sobre una recta se dan los puntos consecutivos A, B y C. Hallar AM2-BM2. Sabiendo que AB*AC=16 y que M es punto medio de BC.
14. Sobre una recta se dan los puntos consecutivos A, B, C y D de modo que AC=12, BD=18. Hallar la longitud del segmento que une los puntos medios de AB y CD.
15. Sobre una recta se tienen los puntos consecutivos R, S, T y U; P y Q son puntos medios de RS y TU respectivamente, si TR= 8cm y SU= 13, calcule: PQ.
16. En una recta se ubican los puntos colineales A, B, C y D. Si AB = 4a, BC = 4 cm y CD = 2a y además AD = 30 cm, calcula la distancia entre los puntos medios de AB y CD.
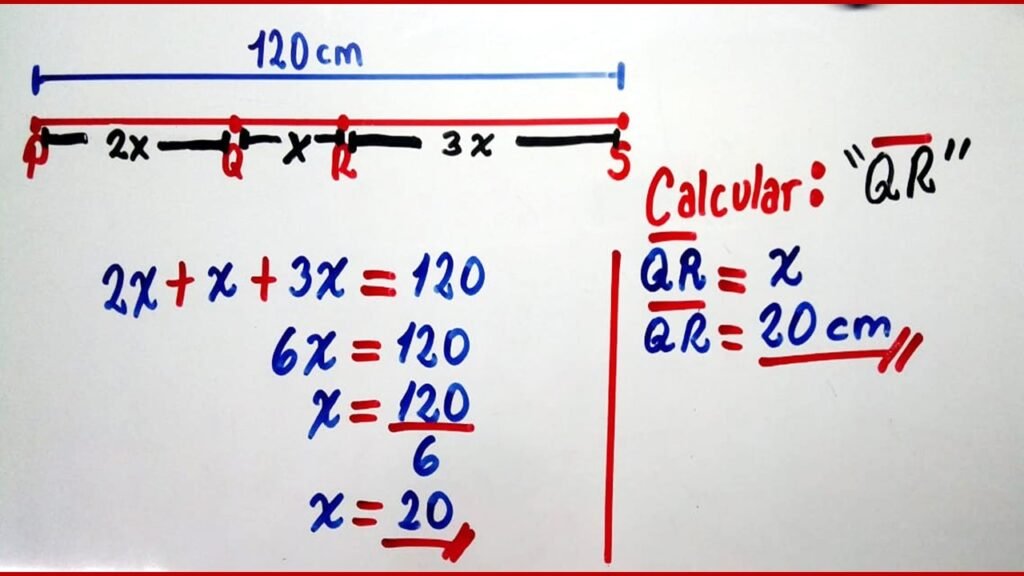
17. P, Q, R y S son puntos colineales y consecutivos, el segmento PS= 120cm el segmento PQ= 2(QR) y el segmento RS=3(QR). Calcular el segmento QR en cm.